Performers: variant of transformer
Random feature for different kernels Softmax: triangnometric, positive Orthogonal features construction: different ways(Givens, Hadamard, regular(GM), or even more), different renormalizations
concentration, computing variance of certain feature map, Cherbychev, concentration results
attention: ..., transformer, MLP, resnet, ...
Markov's inequality
\[ \mathbb{P}(Z\geq t) \leq \frac{\mathbb{E}[Z]}{t} , t\geq 0\] Proof: \[ \mathbb{P}(Z\geq t) = E[1\{Z\geq t\}] \leq E[\frac{Z}{t}]=\frac{\mathbb{E}[Z]}{t} \]
Chebyshev's inequality
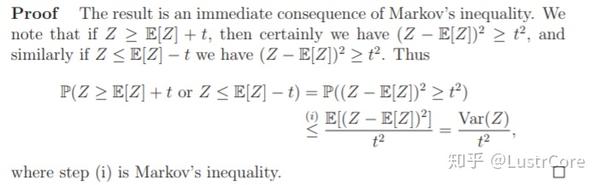## Hoeffding's inequality