豁蒙楼

谈判案例模拟：Leckenby Company

发表于 分类于 Disqus：

概述

Managerial Negotiation 第五周的案例，强调了在谈判前要发现双方共同利益、maximize value creation。在本案例情境中，谈判轮数增加会导致双方可变成本增加，且谈判核心-\(w\)值的增加会导致双方总福利的降低。在设计本模拟工具时也考虑了两种情况：

  • 君子条约: 在罢工（即造成双方成本增加）开始前确定\(w\)在 \(0.5-0.52\) 范围内，对两者较为公平且最大化总价值
  • 消耗战(War of Attrition): 通过模拟发现作为Kunzler(希望w小)，利用前两轮压价、第三轮结束通常能获得最好结果，但该结果仍比君子条约差；作为Arnold(希望w大)，第六轮后结果比君子条约差，但在此之前有较大的议价空间。没有达成君子条约默契并消耗至第六轮，最终结果\(w\)通常在0.6左右，Arnold小赚而Kunzler较亏

针对消耗战情况，又设计了一个函数find_Case来针对当前已知信息（轮数，己方出价，对方出价），找出一个模拟情况，从而对未来局势有所判断。

1
def find_Case(round, w_K, w_A)

案例材料

代码部分

Import

1
2
3
4
5
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import scipy.stats as spst

Simulation1

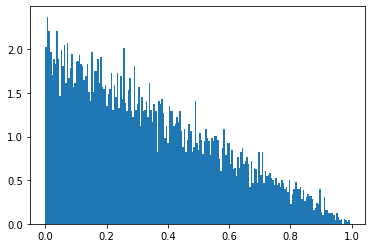
Distribution: triangular(0,0,1)

1
h = plt.hist(np.random.triangular(0, 0, 1, 10000),bins = 200, density=True)

Simulation Code

As two parties approaching the final \(w\), they do not calculate their gain&loss in each round. The next bid is solely subject to the triangular distribution

1
2
3
4
5
6
7
# bid_Kunzler = 10
# bid_Arnold = 11
# round = 0
# while ((bid_Kunzler+0.0004 < bid_Arnold) & (round <=22)):
#     round += 1
#     bid_Kunzler += (bid_Arnold - bid_Kunzler)*np.random.triangular(0, 0.4, 1)
#     bid_Arnold -= (bid_Arnold - bid_Kunzler)*np.random.triangular(0, 0.2, 1)
1
# np.around(bid_Kunzler, 3,), np.around(bid_Arnold, 3,)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def Kunzler(w, d):
    return -5*w -(0.1*d + 0.015*d**2)
def Arnold(w, d):
    return 4*w - (0.05*d + 0.005*d**2)
def simulation():
    bid_Kunzler = 10
    bid_Arnold = 11
    round = 0
    while ((bid_Kunzler+0.0004 < bid_Arnold) & (round <=22)):
        round += 1
        if (np.random.random()>0.2): # 20% chance stick to the previous bid
            bid_Kunzler += (bid_Arnold - bid_Kunzler)*np.random.triangular(0, 0, 1)
        if (np.random.random()>0.2):
            bid_Arnold -= (bid_Arnold - bid_Kunzler)*np.random.triangular(0, 0, 1)
    round -= 1
    if round==22:
        w = 0
    else:
        w = np.around(bid_Kunzler, 3) - 10

    d = (round > 2)*(round - 2)

    return (round, w, Kunzler(w, d), Arnold(w, d))

Run Simulation 100000 times

1
sim = np.array([simulation() for i in range(100000)])
1
df_sim = pd.DataFrame(sim, columns = ["round", "w", "Kunzler", "Arnold"])
1
df_sim = df_sim.assign(total = lambda x: x.Kunzler + x.Arnold)

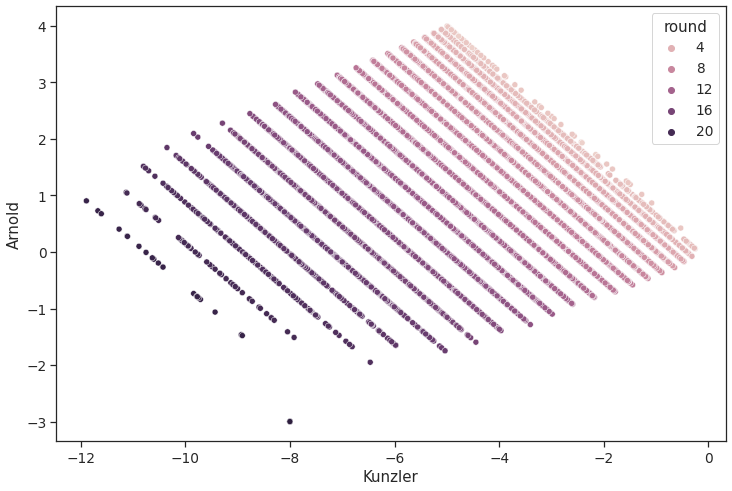
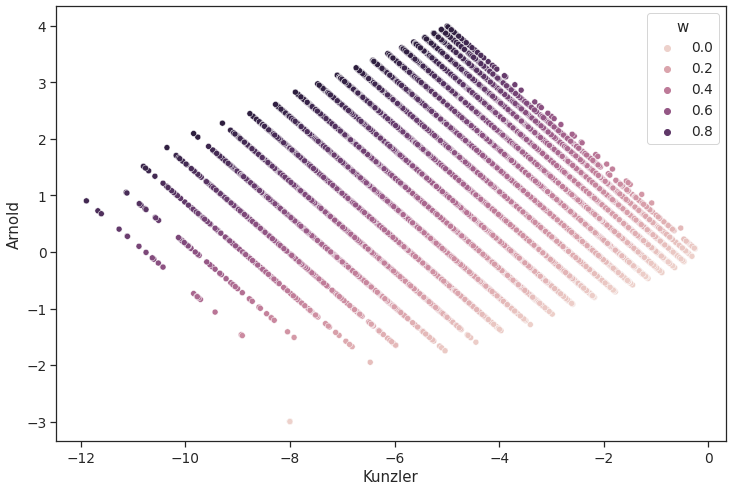
Scatterplot (Kunzler, Arnold), hue="round" / "w"

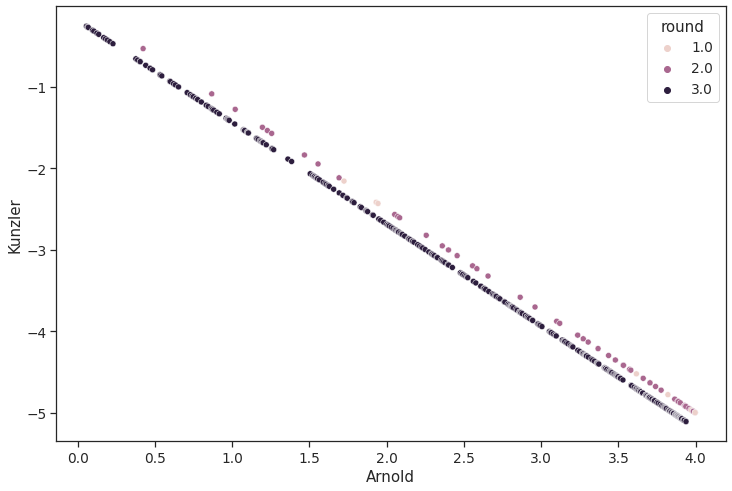
1
2
3
plt.figure(figsize=(12,8))
sns.scatterplot(data=df_sim, x="Kunzler", y="Arnold", hue="round")
plt.show()

1
2
3
plt.figure(figsize=(12,8))
sns.scatterplot(data=df_sim, x="Kunzler", y="Arnold", hue="w")
plt.show()

Analysis

1
df_sim.sort_values(["round", "Kunzler"]).groupby("round").agg("mean")
w Kunzler Arnold total
round
1.0 0.750143 -3.750714 3.000571 -0.750143
2.0 0.741615 -3.708077 2.966462 -0.741615
3.0 0.645737 -3.343684 2.527947 -0.815737
4.0 0.645440 -3.487198 2.461759 -1.025440
5.0 0.615148 -3.510739 2.265591 -1.245148
6.0 0.603678 -3.658389 2.134711 -1.523678
7.0 0.590758 -3.828791 1.988033 -1.840758
8.0 0.584565 -4.062823 1.858259 -2.204565
9.0 0.575110 -4.310551 1.705441 -2.605110
10.0 0.571312 -4.616559 1.565247 -3.051312
11.0 0.569395 -4.961974 1.422579 -3.539395
12.0 0.561997 -5.309983 1.247986 -4.061997
13.0 0.556362 -5.696812 1.070450 -4.626362
14.0 0.552071 -6.120357 0.888286 -5.232071
15.0 0.559690 -6.633452 0.743762 -5.889690
16.0 0.546763 -7.073814 0.507051 -6.566763
17.0 0.540981 -7.579907 0.288926 -7.290981
18.0 0.540375 -8.141877 0.081502 -8.060375
19.0 0.532353 -8.696763 -0.165590 -8.862353
20.0 0.581473 -9.567364 -0.194109 -9.761473
21.0 0.622667 -10.428333 -0.264333 -10.692667
22.0 0.000000 -8.000000 -3.000000 -11.000000

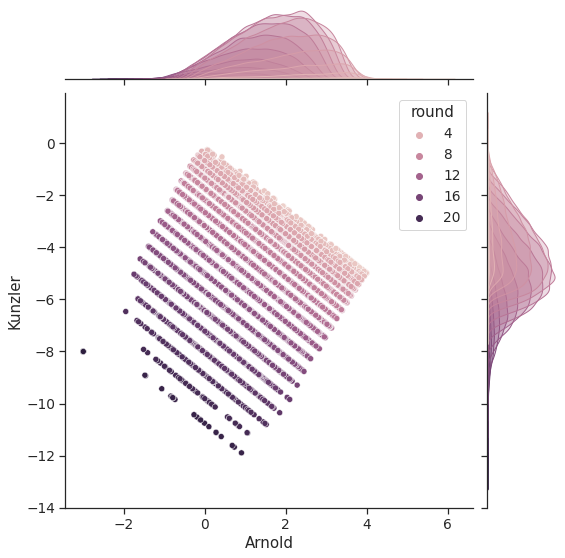
Try to end it early... The upperright midpoint looks good

1
2
3
sns.set_theme(style="ticks", font_scale=1.25,)
sns.jointplot(data=df_sim, y="Kunzler", x="Arnold", hue="round",height=8)
plt.show()
/usr/local/lib/python3.6/dist-packages/seaborn/distributions.py:305: UserWarning: Dataset has 0 variance; skipping density estimate.
  warnings.warn(msg, UserWarning)
/usr/local/lib/python3.6/dist-packages/seaborn/distributions.py:305: UserWarning: Dataset has 0 variance; skipping density estimate.
  warnings.warn(msg, UserWarning)

If we end early before round3, what would be a good proposition? Answer: \(w\in [0.5,0.53]\)

1
df_early = df_sim.loc[df_sim["round"]<=3].sort_values("total", ascending=False)
1
(df_early["Kunzler"].min() + df_early["Kunzler"].max()) / 2
-2.6799999999999997
1
(df_early["Arnold"].min() + df_early["Arnold"].max()) / 2
2.026500000000002
1
Arnold(0.53,0), Kunzler(0.53,0)
(2.12, -2.6500000000000004)
1
Arnold(0.5,0), Kunzler(0.5,0)
(2.0, -2.5)
1
2
3
plt.figure(figsize=(12,8))
sns.scatterplot(data=df_early, x="Arnold", y="Kunzler", hue="round")
plt.show()

Simulation 2: What if my counterpart does not end early?

Another simulation function: Exhibits the process of negotiation

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def simulation(): # Exhibits the process of negotiation
    bid_Kunzler = 10
    bid_Arnold = 11
    round = 0
    # p_Kunzler = 0
    # p_Arnold = 0
    rows = []

    while ((bid_Kunzler+0.004 < bid_Arnold) & (round <=22)):
        round += 1
        if (np.random.random()>0.2): # 20% chance stick to the previous bid
            bid_Kunzler += (bid_Arnold - bid_Kunzler)*np.random.triangular(0, 0, 1)
        if (np.random.random()>0.2):
            bid_Arnold -= (bid_Arnold - bid_Kunzler)*np.random.triangular(0, 0, 1)
        w_Kunzler = bid_Kunzler- 10
        w_Arnold = bid_Arnold-10
        d = (round > 2)*(round - 2)
        Kunzler_ = Kunzler(w_Kunzler, d)
        Arnold_ = Arnold(w_Arnold, d)
        rows.append(np.array([round, w_Kunzler, w_Arnold, Kunzler_, Arnold_]))
    df = pd.DataFrame(np.array(rows), columns = ["round", "w_Kunzler", "w_Arnold", "Kunzler_", "Arnold_"])
    df = df.assign(sum = lambda x: x.Kunzler_ + x.Arnold_)
    return df
1
simulation()
round w_Kunzler w_Arnold Kunzler_ Arnold_ sum
0 1.0 0.000000 0.868807 0.000000 3.475230 3.475230
1 2.0 0.000000 0.420516 0.000000 1.682066 1.682066
2 3.0 0.000297 0.420516 -0.116485 1.627066 1.510581
3 4.0 0.107588 0.201068 -0.797939 0.684272 -0.113667
4 5.0 0.132680 0.157974 -1.098401 0.436896 -0.661505
5 6.0 0.147227 0.156502 -1.376134 0.346006 -1.030128
6 7.0 0.149804 0.156216 -1.624022 0.249866 -1.374156
7 8.0 0.151529 0.156216 -1.897647 0.144866 -1.752782
8 9.0 0.155463 0.155972 -2.212317 0.028890 -2.183427

Tool for finding a similar case(round, w_K, w_A) when negotiating

1
Arnold(0, 20)
-3.0
1
Kunzler(0, 20)
-8.0
1
2
3
4
5
6
7
8
9
10
11
def find_Case(round, w_K, w_A):
    while(True):
        df = simulation()
        try:
            row = df.iloc[round-1]
            flag = (np.abs(row["w_Kunzler"]-w_K)<0.01) & (np.abs(row["w_Arnold"]-w_A)<0.01)
        except:
            flag = False
        if (flag):
            break
    return df
1
find_Case(1, 0, 1)
round w_Kunzler w_Arnold Kunzler_ Arnold_ sum
0 1.0 0.000000 1.000000 0.000000 4.000000 4.000000
1 2.0 0.000000 1.000000 0.000000 4.000000 4.000000
2 3.0 0.382837 0.997914 -2.029186 3.936654 1.907469
3 4.0 0.387834 0.603973 -2.199168 2.295893 0.096725
4 5.0 0.495310 0.586222 -2.911552 2.149887 -0.761664
5 6.0 0.529410 0.584511 -3.287050 2.058045 -1.229006
6 7.0 0.529410 0.579932 -3.522050 1.944727 -1.577323
7 8.0 0.533581 0.579932 -3.807903 1.839727 -1.968176
8 9.0 0.541261 0.577473 -4.141303 1.714890 -2.426413
9 10.0 0.541261 0.577473 -4.466303 1.589890 -2.876413
10 11.0 0.541261 0.575655 -4.821303 1.447619 -3.373685
11 12.0 0.572203 0.575655 -5.361013 1.302619 -4.058394 
1
find_Case(2, 0, 1)
round w_Kunzler w_Arnold Kunzler_ Arnold_ sum
0 1.0 0.000000 1.000000 0.000000 4.000000 4.000000
1 2.0 0.000000 1.000000 0.000000 4.000000 4.000000
2 3.0 0.000000 0.470998 -0.115000 1.828994 1.713994
3 4.0 0.000000 0.337204 -0.260000 1.228817 0.968817
4 5.0 0.000000 0.094733 -0.435000 0.183932 -0.251068
5 6.0 0.000000 0.094733 -0.640000 0.098932 -0.541068
6 7.0 0.000000 0.072679 -0.875000 -0.084283 -0.959283
7 8.0 0.009111 0.068337 -1.185556 -0.206651 -1.392207
8 9.0 0.044854 0.058973 -1.659270 -0.359107 -2.018377
9 10.0 0.047908 0.056863 -1.999541 -0.492550 -2.492091
10 11.0 0.048806 0.055739 -2.359032 -0.632043 -2.991074
11 12.0 0.048806 0.052226 -2.744032 -0.791096 -3.535128 
1
find_Case(4, 0.3, 0.6)
round w_Kunzler w_Arnold Kunzler_ Arnold_ sum
0 1.0 0.155860 0.919539 -0.779300 3.678158 2.898858
1 2.0 0.262073 0.819940 -1.310366 3.279758 1.969392
2 3.0 0.304963 0.808350 -1.639815 3.178401 1.538586
3 4.0 0.304963 0.597116 -1.784815 2.268465 0.483650
4 5.0 0.400535 0.532053 -2.437677 1.933211 -0.504466
5 6.0 0.400584 0.417896 -2.642919 1.391584 -1.251335
6 7.0 0.412972 0.415010 -2.939859 1.285039 -1.654820

Do not concede before Round 4!!!

1
2
%cd /content/drive/My Drive/20FA
!jupyter nb