豁蒙楼

十大排序算法

发表于 更新于 分类于 Disqus：

链接：

十大经典排序算法动画与解析，看我就够了！（配代码完全版）

视频 | 手撕九大经典排序算法，看我就够了！ - 力扣（LeetCode）的文章 - 知乎

复杂度

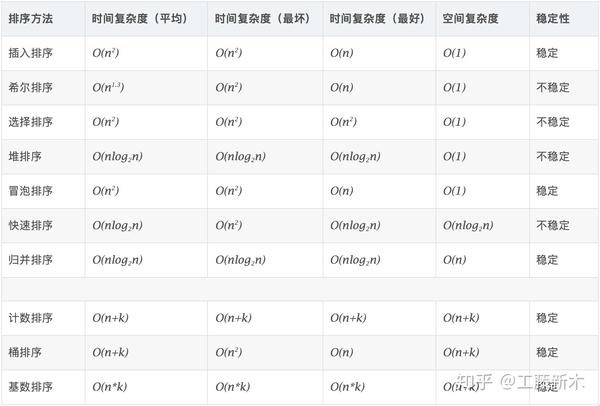
复杂度

很多高效排序算法的代价是 nlogn，难道这是排序算法的极限了吗？ - 曾加的回答 - 知乎

排序算法

冒泡排序

基础版本： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import Java.util.Arrays;
public static int[] BubbleSort(int[] sourceArray) {
    int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
    int temp;

    for (int i = 0; i < arr.length; i++) {
        for (int j = 0; j < arr.length - i - 1; j++) {
            if (arr[j + 1] < arr[j]) {
                temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
    return arr;
}

优化版本： 如果第i个循环，从第0个到第arr.length-1-i都顺序，则可以提前结束 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public static int[] BubbleSort(int[] sourceArray) {
    int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
    int temp;
    boolean flag;

    for (int i = 0; i < arr.length; i++) {
        flag = true; // 默认存在逆序对，会发生交换
        for (int j = 0; j < arr.length - i - 1; j++) {
            if (arr[j + 1] < arr[j]) {
                flag = false;
                temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
        if (flag) 
            break; //如果全部顺序就提前结束外循环
    }
    return arr;
}

选择排序

每一步找出未排序序列中的最小值 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public static int[] SelectionSort(int[] sourceArray){
    int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
    for (int i = 0; i < arr.length; i++){
        int argmin = i;
        for (int j = i; j < arr.length; j++){
            if (arr[j] < arr[argmin]){
                argmin = j;
            }
        }
        int temp = arr[i];
        arr[i] = arr[argmin];
        arr[argmin] = temp;
    }
    return arr;
}

插入排序

把下一个元素插入到有序序列的合适位置 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public static int[] InsertSort(int[] sourceArray){
    int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
    for (int i = 1; i < arr.length; i++){
        int j = i;
        int temp = arr[i];
        while (j - 1 >= 0 && arr[j - 1] > temp){
            arr[j] = arr[j-1];
            j--;
        }
        arr[j] = temp;
    }
    return arr;
}

希尔排序

优化版的插入排序 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public static int[] ShellSort(int[] sourceArray) {
    int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
    for (int gap = arr.length >> 1; gap >= 1; gap >>= 1) {
        for (int i = gap; i < arr.length; i++) {
            int temp = arr[i];
            int j = i;
            while (j - gap >= 0 && arr[j - gap] > temp) {
                arr[j] = arr[j - gap];
                j -= gap;
            }
            arr[j] = temp;
        }
    }
    return arr;
}

归并排序

递归，如果用原位迭代空间复杂度为o(1)但时间复杂度到o(n2) 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
public static int[] MergeSort(int[] sourceArray) {
    int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);

    if (arr.length < 2)
        return arr;

    int middle = arr.length >> 1;
    int[] left = Arrays.copyOfRange(arr, 0, middle);
    int[] right = Arrays.copyOfRange(arr, middle, arr.length);

    return merge(MergeSort(left), MergeSort(right));
}

static int[] merge(int[] left, int[] right) {// 两个有序序列
    int[] result = new int[left.length + right.length];
    int i = 0;
    while (left.length > 0 && right.length > 0) {
        if (left[0] <= right[0]) {
            result[i] = left[0];
            i++;
            left = Arrays.copyOfRange(left, 1, left.length);
        } else {
            result[i] = right[0];
            i++;
            right = Arrays.copyOfRange(right, 1, right.length);
        }
    }

    while (left.length > 0) {
        result[i] = left[0];
        i++;
        left = Arrays.copyOfRange(left, 1, left.length);
    }
    while (right.length > 0) {
        result[i] = right[0];
        i++;
        right = Arrays.copyOfRange(right, 1, right.length);
    }

    return result;
}

快速排序

  • 快速排序是对冒泡排序的一种改进。
  • 时间复杂度并不固定，如果在最坏情况下（元素刚好是反向的）速度比较慢，达到 O(n^2)（和选择排序一个效率），但是如果在比较理想的情况下时间复杂度 O(nlogn)。
QuickSort
  • 从数列中挑出一个元素，称为 “基准”（pivot）;
  • 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。
  • 如果基准值pivot在最左，从i=index=pivot+1开始，每次遇到比arr[index]小的元素，就swap(arr, i, index); index++。index记录分隔符向右移动的情况，但此时pivot的位置还未改变，直到最后再swap(arr), pivot, index-1。
  • 在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
  • 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public static int[] QuickSort(int[] sourceArray) {
        int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
        return quicksort(arr, 0, arr.length - 1);
    }

static int[] quicksort(int[] arr, int left, int right) {
    if (left < right) { // 约束，防止partitionIndex到0
        int partitionIndex = partition(arr, left, right); // partition实际执行排序操作
        quicksort(arr, left, partitionIndex - 1); // 不含中间
        quicksort(arr, partitionIndex + 1, right);
    }
    return arr;
}

// partition方法对arr进行修改
static int partition(int[] arr, int left, int right) {
    int pivot = left;
    int index = pivot + 1; // 从左端开始
    for (int i = index; i <= right; i++) {
        if (arr[i] < arr[pivot]) {
            swap(arr, i, index); // pivot右边一位作为index不断地和后续比arr[pivot]小的元素交换位置，
            index++; // index位向右挪
            // 最终pivot往右直到index-1都是小于基准的，再把pivot放到中间位置index-1
        }
    }
    swap(arr, pivot, index - 1);
    return index - 1;
}

static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

堆排序

  • 堆：相较于完全二叉树，所有父节点的值大于（小于）子节点
  • 最大堆的最大元素值出现在根结点（堆顶）
  • 稳定性：不稳定
  • 完全二叉树、二叉堆属于数据结构。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
static void heapify(int[] arr, int i, int len){
    int left = 2 * i + 1;
    int right = 2 * i + 2;
    int largest = i;

    if (left < len && arr[left] > arr[largest] ){ //注意次序，先判断index
        largest = left;
    }
    if (right < len && arr[right] > arr[largest]){
        largest = right;
    }

    if (i < largest){
        swap(arr, i, largest);
        heapify(arr, largest, len);
    }
}

static void buildMaxHeap(int[] arr, int len){
    for (int i = len >> 1; i >= 0; i--){ //i >= 0
        heapify(arr, i, len);
    }
}

static int[] heapSort(int[] sourceArray){
    int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
    int len = arr.length;

    buildMaxHeap(arr, len);
    for (int i = len - 1; i > 0; i--){
        swap(arr, 0, i); // 右下子节点和根节点交换，根节点最大值放到最后
        len--;
        heapify(arr, 0, len); //调整堆
    }
    return arr;
}

static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

计数排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
static int[] CountingSort(int[] sourceArray){
        int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
        return (countingsort(arr, getMaxValue(arr)));
    }
    
static int[] countingsort(int[] arr, int maxValue){
    int bucketlen = maxValue + 1;
    int[] bucketarr = new int[bucketlen];
    for (int value: arr){
        bucketarr[value] ++;
    }
    int sortedIndex = 0;
    for (int i = 0; i < bucketlen; i++){ // i < bucketlen
        while (bucketarr[i]>0){
            arr[sortedIndex++] = i;
            bucketarr[i]--;
        }
    }
    return arr;
}

static int getMaxValue(int[] arr){
    int maxValue = arr[0];
    for (int i = 1; i < arr.length; i++){
        maxValue = arr[i] > maxValue ? arr[i] : maxValue;
    }
    return maxValue;
}

桶排序

BucketSort
  • 设置固定数量的空桶。
  • 把数据放到对应的桶中
  • 对每个不为空的桶中数据进行排序
  • 拼接不为空的桶中数据，得到结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
public class BucketSort {
    public static void main(String[] args) {
        int[] a = { 9, 8, 7, 6, 5, 4, 3, 2, 1 };
        System.out.println(Arrays.toString(sort(a)));
    }

    public static int[] sort(int[] sourceArray) {
        int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
        return bucketSort(arr, 5);
    }

    //桶排序主体部分 
    static int[] bucketSort(int[] arr, int bucketSize) {
        if (arr.length == 0)
            return arr;

        int maxValue = arr[0];
        int minValue = arr[0];

        for (int value : arr) {
            maxValue = value > maxValue ? value : maxValue;
            minValue = value < minValue ? value : minValue;
        }

        int bucketCount = (int) Math.floor((maxValue - minValue) / bucketSize) + 1;
        int[][] buckets = new int[bucketCount][0];

        for (int value : arr) {
            int bucketIndex = (int) Math.floor((value - minValue) / bucketSize);
            buckets[bucketIndex] = arrayAppend(buckets[bucketIndex], value);
        }

        int sortedIndex = 0;
        for (int i = 0; i < bucketCount; i++) {
            if (buckets[i].length == 0) {
                continue;
            }

            int[] bucket = buckets[i];
            bucket = InsertSort(bucket);

            for (int j = 0; j < bucket.length; j++) {
                arr[sortedIndex++] = bucket[j];
            }
        }
        return arr;
    }

    // 每个桶内部用到插入排序
    static int[] InsertSort(int[] sourceArray) {
        int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
        for (int i = 1; i < arr.length; i++) {
            int j = i;
            int temp = arr[j];
            while (j > 0 && arr[j - 1] > temp) {
                arr[j] = arr[j - 1];
                j--;
            }
            arr[j] = temp;
        }
        return arr;
    }

    static void swap(int[] arr, int a, int b) {
        int temp = arr[a];
        arr[a] = arr[b];
        arr[b] = temp;
    }

    // array扩容
    static int[] arrayAppend(int[] arr, int a) {
        arr = Arrays.copyOf(arr, arr.length + 1);
        arr[arr.length - 1] = a;
        return arr;
    }
}

基数排序

  • 首先通过getMaxValue方法得出最大数
  • 通过getDigitCount方法得出最大数的数位数，也就是全arr的最大digits数
  • getDigitValue方法可以给出给定数的某数位的值
  • 从低位（个位）开始，新建0-9十个空桶，按照arr中每个数的个位放入桶中，然后再依次放回到arr中
  • 再进入下一位，新建十个空桶，重复操作
  • 直到遍历MaxDigit
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
import java.util.Arrays;

public class RadixSort {
    static int[] sort(int[] sourceArray) {
        int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
        int maxDigit = getMaxDigit(arr);
        return radixSort(arr, maxDigit);
    }

    static int[] radixSort(int[] arr, int maxDigit) {
        // 从个位比较开始数位 (低位)
        for (int i = 0; i < maxDigit; i++) {
            // 每次比较数位时初始化新的10个空桶
            int[][] buckets = new int[10][0]; // 0-9, 10 buckets, each store several values;
            // arr的值进入10个桶
            for (int value : arr) {
                buckets[getDigitValue(value, i)] = arrayAppend(buckets[getDigitValue(value, i)], value);
            }
            // 从桶中把值拿出来放回arr
            int sortedIndex = 0;
            for (int j = 0; j < 10; j++) {
                // System.out.printf("buckets[%d]: %s", j, Arrays.toString(buckets[j]));
                if (buckets[j].length == 0)
                    continue;
                for (int value : buckets[j]) {
                    arr[sortedIndex++] = value;
                }
            }
        }
        return arr;
    }

    // 个位为第0位
    static int getDigitValue(int a, int digit) {
        int digitCount = getDigitCount(a);
        if (digit > digitCount - 1)
            return 0;

        for (int i = 0; i < digit; i++) {
            a /= 10;
        }
        return a % 10;
    }

    static int getMaxDigit(int[] arr) {
        int maxValue = getMaxValue(arr);
        return getDigitCount(maxValue);
    }

    static int getDigitCount(int a) {
        int digitCount = 0;
        while (a > 0) {
            a /= 10;
            digitCount++;
        }
        return digitCount;
    }

    static int getMaxValue(int[] arr) {
        int maxValue = arr[0];
        for (int value : arr) {
            maxValue = value > maxValue ? value : maxValue;
        }
        return maxValue;
    }

    static int[] arrayAppend(int[] arr, int a) {
        arr = Arrays.copyOf(arr, arr.length + 1);
        arr[arr.length - 1] = a;
        return arr;
    }

    public static void main(String[] args) {
        int[] a = { 9, 28, 7, 345, 579, 42, 3, 2, 101 };
        System.out.println(Arrays.toString(sort(a)));
    }

}